LAMMPS模拟非晶合金的非局部变形，在超算互联网复现一篇MD模拟文献

LAMMPS是分子动力学模拟领域最强大的工具之一，被广泛应用于材料、化学等研究中。
本次实操，我们将在超算互联网平台使用LAMMPS软件，来复现发表在金属材料顶刊《Acta MATERIALIA》上的一篇纯MD模拟。论文通过大规模原子模拟，研究表明在预先存在非晶剪切带的金属玻璃（MG）中，拉伸下剪切局部化被抑制。
文献提出的材料设计极具奇思妙想，该设计仅能在模拟环境中得以实现，同时文章还对其进行了深入分析。

论文链接：https://doi.org/10.1016/j.actamat.2014.01.003

文献模拟思路

小块CuZr非晶金属玻璃的制备

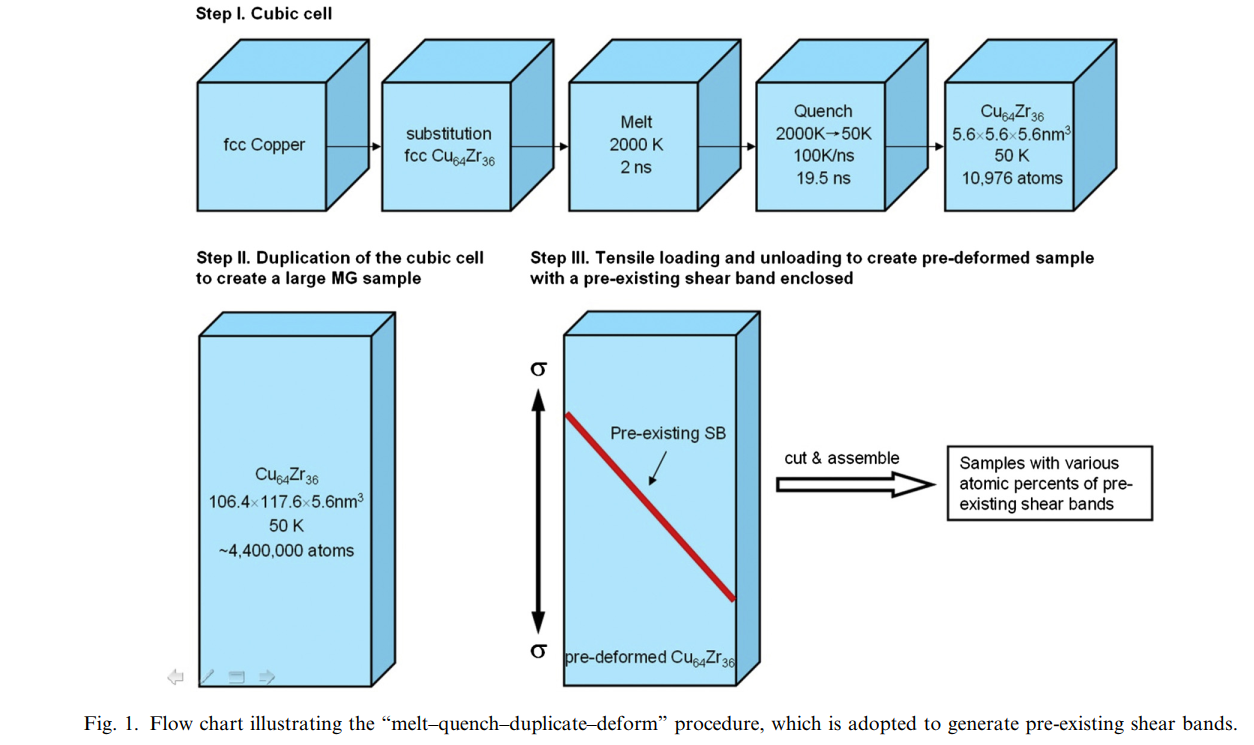
首先我们需要制备一小块CuZr非晶金属玻璃。那么我们只需要撰写如下的输入文件，并提交计算即可：

# 模型的基础设置
units metal
boundary p p p
timestep 0.001
shell mkdir dump
# 建模设置
lattice fcc 3.615
region box block  0 20 0 20 0 20 units lattice
create_box 2 box
create_atoms 1 box
# 替换36%的Cu原子为Zr原子
set type 1 type/ratio 2 0.36 23231
# 势函数设置
pair_style eam/alloy 
pair_coeff * * ZrCu_lammps.eam  Cu Zr
# 导出模型文件查看
write_data CuZr.lmp 
# 为所有原子创建初始温度
velocity all create 2000.0 4928459 mom yes dist gaussian
# 定义热力学输出
thermo 500
thermo_style custom step cpu temp pxx pyy pzz press pe 
# 定义计算一些原子的属性
compute pe all pe/atom 
compute ke all ke/atom
# 在NPT系综下保温弛豫一定的时间
fix 1 all npt temp 2000.0 2000.0 $(100*dt) iso 0.0 0.0 $(1000*dt)
run 1000000
unfix 1
# 从2000k缓慢降温至目标温度
fix 1 all npt temp 2000.0 50.0 $(100*dt) iso 0.0 0.0 $(1000*dt)
dump 1 all custom/gz 100000 dump/relaxing_*.dump.gz id type element mass x y z c_pe c_ke
dump_modify 1 element Cu Zr
run 10000000
# 将模型导出
write_data CuZr_unit.lmp

由于模型不大，所以不需要太多的CPU核数，这里需要注意严格控制降温的速度，建议数量级不要超过10的11次方k（1011K/s）每秒的降温速率。
运行完上述in文件之后，我们就会得到一块非晶CuZr金属玻璃，将其导入OVITO中进行复制扩胞，为我们之后获取剪切带原子做准备，这里可以将扩胞扩大一点，这样后面我们截取剪切带原子的可以选到更多的原子。
打开ovito，将模型导入，添加replicate模块，这里选择的是在Y轴上复制3倍，在Z轴上复制6倍。
获得扩胞之后的模型之后，我们撰写如下的输入文件对模型进行拉伸：

# 非晶CuZr的拉伸模拟
units       metal
boundary    p p p
timestep    0.001
atom_style  atomic
shell mkdir dump

# 读取建模文件
read_data CuZr_bulk.lmp 
change_box all boundary s s p
# 定义势函数
pair_style  eam/alloy
pair_coeff  * * ZrCu_lammps.eam Cu Zr

# 导出模型进行查看
# write_data watch.lmp

# 设置邻居列表
neighbor    1.0 bin
neigh_modify every 10 delay 0 check yes

# 在NPT系综下进行弛豫
thermo      1000
thermo_style custom step cpu temp pxx pyy pzz pxy press pe

velocity    all create 50.0 5812775 mom yes dist gaussian
fix     1 all npt temp 50.0 50.0 $(100*dt) z 0.0 0.0 $(1000*dt)
run     50000
reset_timestep  0
unfix 1

# 定义与应变过程相关的变量
variable rate equal 5e8             # 期望的以s为单位的应变率, 这里是5x10^9 /s
variable trate equal v_rate/1e12  # 对应的在metal单位制下的应变率
variable strain equal 0.4         # 期望施加的最终的拉伸应变
variable Total_step equal round(v_strain/v_trate/dt)  # 需要运行的步数
variable current_strain equal ${trate}*dt*step  # 当前步数下对应的剪切应变
variable tensile_stress equal -pzz/10000           # 单位为GPa的剪切方向上的应力

print "A total of ${Total_step} steps need to be run." 

# 定义新的热力学输出
thermo      1000
thermo_style custom step cpu temp pxx pyy pzz v_current_strain pe

# 开始剪切
fix 1 all nvt temp 50.0 50.0 0.1
fix 2 all deform 50 z erate ${trate} remap x  # 沿着z轴进行deform, deform之后对坐标进行缩放
fix 3 all print 200 "${current_strain} ${tensile_stress}" file unave_stress.txt screen no
fix 4 all ave/time 1000 5 5000 v_current_strain v_tensile_stress off 1 file ave_stress.txt
dump        1 all custom/gz 20000 dump/Tension_*.gz id type element mass x y z 
dump_modify 1 element Cu Zr

run     ${Total_step}

切割获取剪切带与非剪切带原子模型

将轨迹文件从超算中心下载下来。将其导入OVITO中。添加Atomic Strain模块，计算原子应变，并调用Color coding，设置原子应变上下限分别为0.4和0.0。观察模型中的剪切带原子分布情况。
这里我选择第80帧作为获取剪切带原子的轨迹文件，此时模型已经有比较成熟的剪切带了，如下图所示：

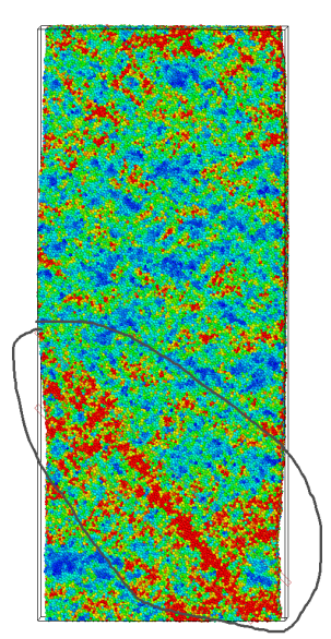
首先调用第一个slice模块，设置平面的法向量为[0 1 1], 平面厚度为50，同时不断调整平面距离，尽量将整个剪切带原子都包含进去。这里选择的距离数值为-35.85，大家可以根据自己的模型进行适当调整。
然后我们插入第二个slice模块，设置平面的法向量为[0 1 -1], 设置平面厚度为250，同时不断调整平面距离，尽量将整个剪切带原子都包含进去。这里我们选择的距离数值为86.15。
接下来我们调用affine transformation，将剩余模型绕x轴旋转-45°。注意这里需要去掉simulation box前面的勾选选项。再通过translation的选项不断调整原子的位置，使得所有原子都位于盒子内部。
最后我们导出模型，注意需要将ignore particle identifiers选项去掉。然后撰写并运行如下的in文件，对模型进行调整：

# 模型的基础设置
units metal
boundary p p p
timestep 0.001
# 建模设置
read_data CuZr_deformed.lmp
# 势函数设置
pair_style eam/alloy 
pair_coeff * * ZrCu_lammps.eam  Cu Zr
# 定义切割原子的时候, 切割出来的矩形形状大小
variable length equal 250
variable width equal 50
# 获取当前原子组分别在x,y,z轴上的左边最小值, 并预留0.1埃的间隙
variable xmin equal -bound(all,xmin)+0.1
variable ymin equal -bound(all,ymin)+0.1
variable zmin equal -bound(all,zmin)+0.1
variable xlen equal lx
# 平移所有原子
displace_atoms all move ${xmin} ${ymin} ${zmin}
# 调整盒子大小
change_box all x final 0 ${xlen}
change_box all y final 0 ${width}
change_box all z final 0 ${length}
# 导出模型
write_data CuZr_deformed.lmp

这样，我们就最终获得了一个完整的剪切带原子模型。它的高为250，宽为50，而厚度则与我们之前拉伸时候的in文件设置有关，这里我的模型的厚度为75.0366。
接下来，我们需要从之前扩胞之后的大块CuZr非晶中，切出一块和上述模型一模一样大小的原子，而这通过atomsk进行操作很简单，首先我们需要一个txt文件，里面内容如下：

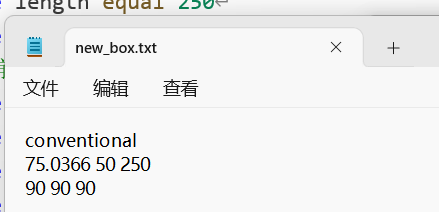
然后，将扩胞之后的模型文件，与上述txt文件放在同一个目录下，运行下述两个命令：
atomsk CuZr_bulk.lmp -select out box 0 0 0 75.0366 50 250 -rmatom select tmp.lmp
atomsk tmp.lmp -properties new_box.txt undeform_CuZr.lmp
这样，得到的undeform_CuZr.lmp就是同样的高为250，宽为50，厚度为75.0366的长方体非晶模型了。
获得上述两个模型之后，我们就可以模仿文献来一次拉伸实验，分别对上述两个模型进行拉伸，拉伸的in文件与文章开头的in文件内容基本一致，仅需要修改read_data之后的模型文件名称即可。然后我们编撰如下的python脚本，进行应力应变曲线的绘制：

import numpy as np
import matplotlib.pyplot as plt

data_deform = np.loadtxt("../deform_glass_tension/ave_stress.txt")
data_normal = np.loadtxt("../undeform_glass_tension/ave_stress.txt")

plt.plot(data_normal[:, 1]*100, data_normal[:, 2], label="As_cast")
plt.plot(data_deform[:, 1]*100, data_deform[:, 2], label="Shear Banded")
plt.xlabel("Strain (%)")
plt.ylabel("Stress (GPa)")
plt.legend()
plt.savefig("stress.png",dpi=600)
plt.show()

绘制结果如下：

拼接剪切/非剪切模型并进行拉伸

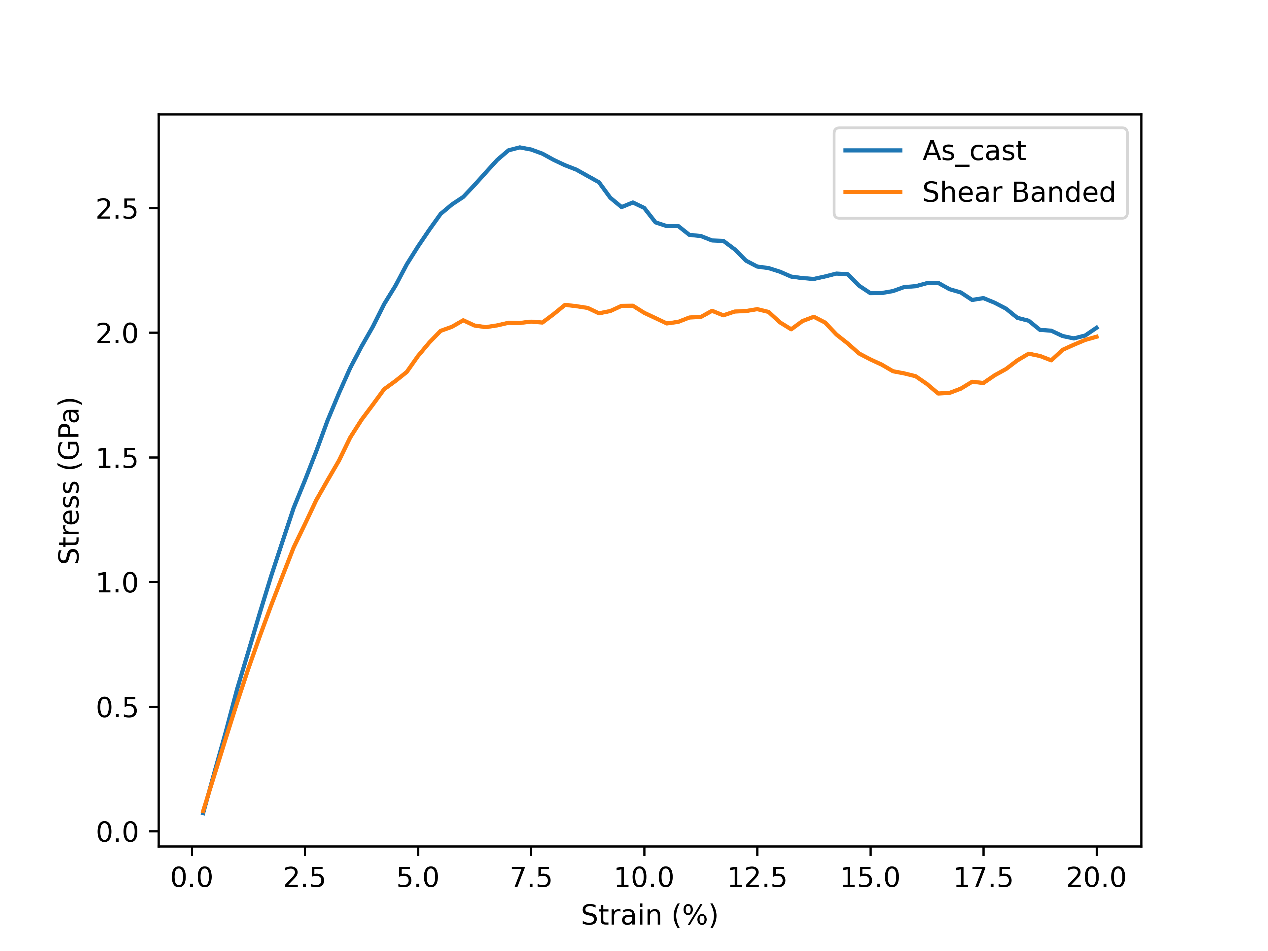
那么自然我们就有一种想法，如果将剪切带模型与非剪切带模型复合到一起，那么我们是否有可能获得一种既有高强度，又兼具良好的应变硬化能力的材料呢？而这个想法同样也是上述顶刊文献的核心想法。
为此，我们可以撰写如下的in文件，同时将刚刚切割出来的变形和未变形的模型文件放到一起，将它们合并起来：

# 非晶CuZr的拉伸模拟
units       metal
boundary    p p p
timestep    0.001
atom_style  atomic
shell mkdir dump

# 读取建模文件
read_data undeform_CuZr.lmp extra/atom/types 2
read_data deformed_CuZr.lmp add append offset 2 0 0 0 0 shift 0.0 50.0 0.0
replicate 1 3 2
change_box all boundary p s p
# 定义势函数
pair_style  eam/alloy
pair_coeff  * * ZrCu_lammps.eam Cu Zr Cu Zr

# 导出模型进行查看
write_data watch.lmp

# 设置邻居列表
neighbor    1.0 bin
neigh_modify every 10 delay 0 check yes

# 在NPT系综下进行弛豫
thermo      1000
thermo_style custom step cpu temp pxx pyy pzz pxy press pe

velocity    all create 50.0 5812775 mom yes dist gaussian
fix     1 all npt temp 50.0 50.0 $(100*dt) z 0.0 0.0 $(1000*dt) x 0.0 0.0 $(1000*dt)
run     50000
reset_timestep  0
unfix 1

# 定义与应变过程相关的变量
variable rate equal 4e8             # 期望的以s为单位的应变率, 这里是5x10^9 /s
variable trate equal v_rate/1e12  # 对应的在metal单位制下的应变率
variable strain equal 0.2         # 期望施加的最终的拉伸应变
variable Total_step equal round(v_strain/v_trate/dt)  # 需要运行的步数
variable current_strain equal ${trate}*dt*step  # 当前步数下对应的剪切应变
variable tensile_stress equal -pzz/10000           # 单位为GPa的剪切方向上的应力

print "A total of ${Total_step} steps need to be run." 

# 定义新的热力学输出
thermo      1000
thermo_style custom step cpu temp pe pxx pyy pzz v_current_strain v_tensile_stress 

# 开始剪切
fix 1 all npt temp 50.0 50.0 $(100*dt) x 0.0 0.0 $(1000*dt)
fix 2 all deform 500 z erate ${trate} remap x  # 沿着z轴进行deform, deform之后对坐标进行缩放
fix 3 all print 200 "${current_strain} ${tensile_stress}" file unave_stress.txt screen no
fix 4 all ave/time 1000 5 5000 v_current_strain v_tensile_stress off 1 file ave_stress.txt
dump        1 all custom/gz 20000 dump/Tension_*.gz id type element mass x y z 
dump_modify 1 element Cu Zr Ta Fe

run     ${Total_step}

这里需要注意的是，为了区分剪切带原子和非剪切带原子，我将非剪切带原子分别定义为Cu和Zr，剪切带原子定义为Ta和Fe，运行上述文件可以得到如下模型：

这样我们就得到了剪切带和非剪切带相互交替的模型，然后上述in文件会对这个模型进行拉伸。并获取其应力应变曲线。
此外我们还多做了一个模型，那就是将模型水平方向进行堆叠：

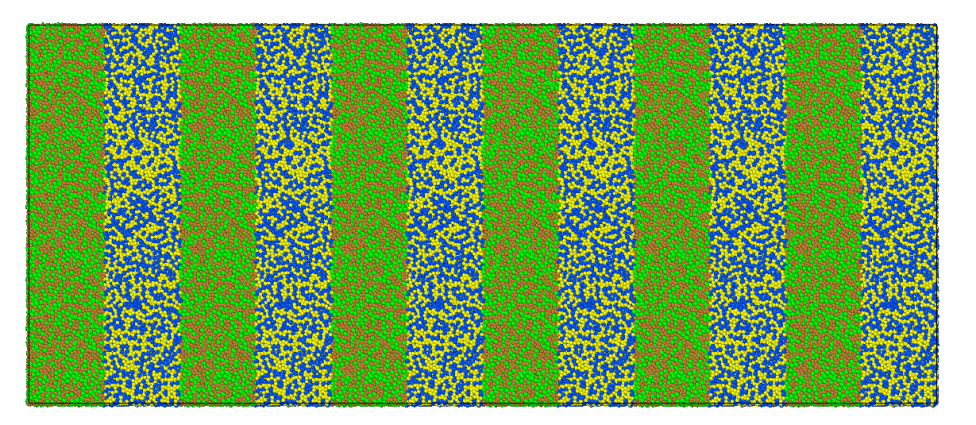
这两个模型的原子数量都是完全一样，只不过一个拉伸方向平行与堆叠方向，一个拉伸方向垂直于堆叠方向。拉伸的in文件则基本一致。提交in文件的过程这里不再赘述。

利用python对结果进行简单处理

得到结果之后，我们来撰写如下的python脚本文件：

import numpy as np
import matplotlib.pyplot as plt

# 创建一个包含1行2列子图的图形
fig, axes = plt.subplots(1, 2, figsize=(10, 5))
# 读取数据文件
data_deform = np.loadtxt("../deform_glass_tension/ave_stress.txt")
data_normal = np.loadtxt("../undeform_glass_tension/ave_stress.txt")
data_vertical = np.loadtxt("../composite_vertical/ave_stress.txt") 
data_horizon = np.loadtxt("../composite_horizental/ave_stress.txt") 
data_as_cast = np.loadtxt("../CuZr_Bulk/ave_stress.txt")
# 绘制第一张子图
axes[0].plot(data_normal[:, 1]*100, data_normal[:, 2], label="As_cast")
axes[0].plot(data_deform[:, 1]*100, data_deform[:, 2], label="Shear Banded")
axes[0].set_xlabel("Strain (%)")
axes[0].set_ylabel("Stress (GPa)")
axes[0].legend()
# 绘制第二张子图
axes[1].plot(data_vertical[:, 1]*100, data_vertical[:, 2], label="Vertical")
axes[1].plot(data_horizon[:, 1]*100, data_horizon[:, 2], label="horizon")
axes[1].plot(data_as_cast[:, 1]*100, data_as_cast[:, 2], label="Homogenous")
axes[1].set_xlabel("Strain (%)")
axes[1].set_ylabel("Stress (GPa)")
axes[1].legend()
# 调整子图之间的间距
plt.tight_layout()
plt.savefig("stress.png",dpi=600)
plt.show()

将脚本文件命名为plot.py，在终端输入python plot.py，就会得到如下的应力应变曲线：

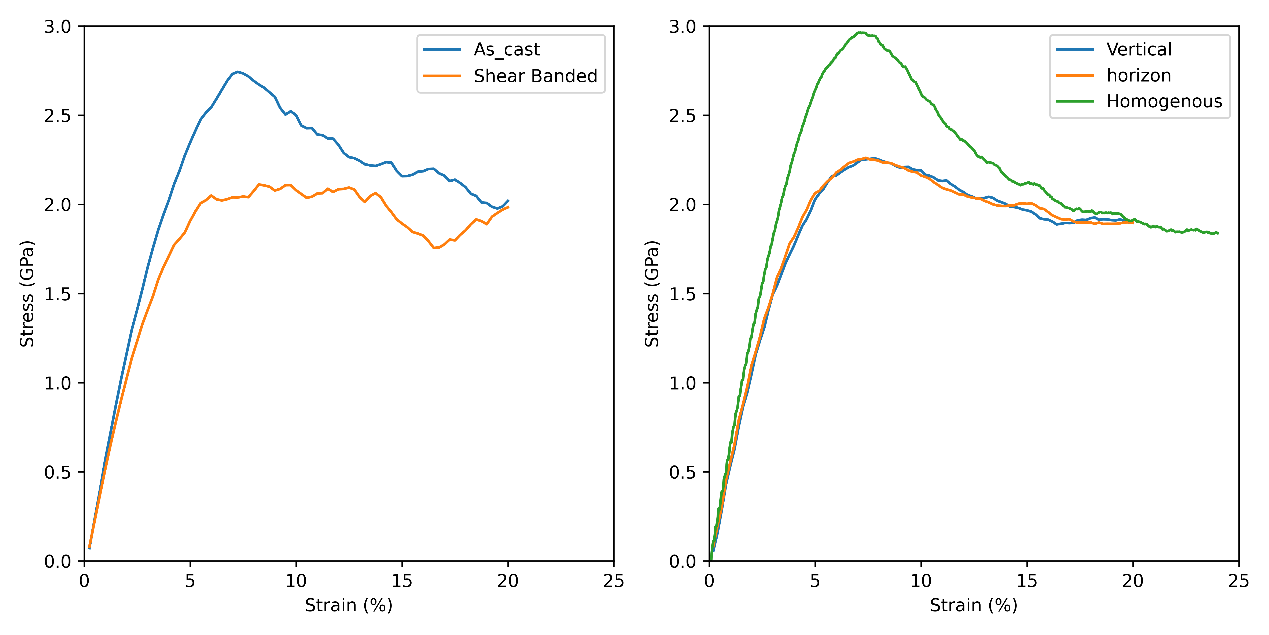
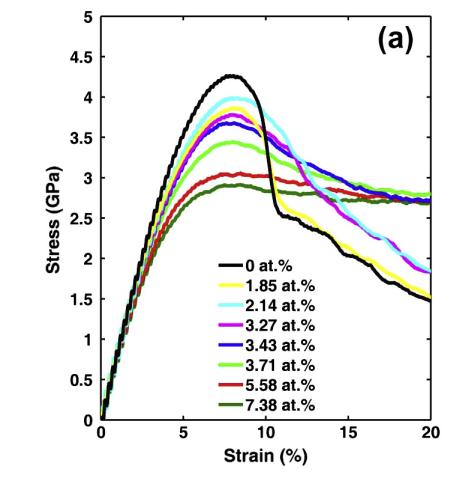
其中，第一个子图对应的是之前的剪切带模型和非剪切带的应力曲线。第二个子图中，绿色曲线为均质非晶玻璃模型的拉伸曲线。
相比之下，这种新型的复合材料可能具有良好的塑性变形能力。与文献一致。
此外，可以发现，通过引入了非剪切带模型之后，样品的强度得到了一定程度的提高。与预期相符。
最后让我们来看看复合模型中的剪切原子分布情况。
将均质模型导入ovito，先调用atomic strain，设置cutoff radius为3.5，然后设置color coding，下限为0，上限为0.4。
可以看到，在25%应变下，模型已经出现了一条较为明显的主剪切带了，与拉伸大致成45°夹角。说明该样品已经出现了剪切集中，塑性变形能力较差。
然后我们把界面平行于拉伸方向的模型导入，观察25%应变下的模型，可以看到该模型的大剪切应变原子分布较为均匀，说明该样品克服了应变局域化的缺陷，具有良好的塑性变形能力。
然后我们导入另外一个界面垂直于拉伸方向的模型轨迹文件，发现大剪切应变原子的分布情况也是差不多，分布均匀，无明显的主剪切带形成。
至此，我们的文献复现也差不多完成了。
由于时间关系，这里只选取了文献中最具代表性的几个模型进行复现。但是大家应该可以根据文章中的教程来完成剩余的模型的仿真。